May 31, 2006
Bayesian probability and quantum mechanics
Also related:
http://math.ucr.edu/home/baez/bayes.html
http://plato.stanford.edu/archives/sum2003/entries/probability-interpret/
http://bayesrules.net/ast383.html
http://math.ucr.edu/home/baez/
http://math.ucr.edu/home/baez/questions.html
http://math.ucr.edu/home/baez/physics/
http://www.cs.uwaterloo.ca/~alopez-o/math-faq/math-faq.html
Full post... Related link
May 30, 2006
Diaspora by Greg Egan
... novel combinations of symbols were firing all the time, and if they resonated strongly enough with the current activity, their alliance could be reinforced, and even rise to consciousness. Thought was a lot like biochemistry; there were millions of random collisions going on all the time, but it was the need to form a product with the right shape to adhere firmly to an existing template that advanced the process in a coherent way.
Full post... Related link
May 24, 2006
How to daemonize slow startup processes
Full post...
May 09, 2006
Amino acid codes and types
- http://www.ebi.ac.uk/2can/tutorials/aa.html
- http://www.ebi.ac.uk/2can/biology/molecules_small_aatable.html
- http://www.ebi.ac.uk/2can/biology/trans2.html
- http://www.cmbi.kun.nl/gvteach/aainfo/struct.shtml
- http://www.cmbi.kun.nl/gvteach/aainfo
The one-letter and three-letter abbreviation codes for amino acids for example, used in UniProtKB/Swiss-Prot are those adopted by the commission on Biochemical Nomenclature of the IUPAC-IUB and are as follows (numbers give frequencies):
A Ala 7.49 Alanine
R Arg 5.22 Arginine
N Asn 4.53 Asparagine
D Asp 5.22 Aspartic acid
C Cys 1.82 Cysteine
Q Gln 4.11 Glutamine
E Glu 6.26 Glutamic acid
G Gly 7.10 Glycine
H His 2.23 Histidine
I Ile 5.45 Isoleucine
L Leu 9.06 Leucine
K Lys 5.82 Lysine
M Met 2.27 Methionine
F Phe 3.91 Phenylalanine
P Pro 5.12 Proline
S Ser 7.34 Serine
T Thr 5.96 Threonine
W Trp 1.32 Tryptophan
Y Tyr 3.25 Tyrosine
V Val 6.48 Valine
B Asx Aspartic acid or Asparagine
Z Glx Glutamic acid or Glutamine
X Xaa Any amino acid
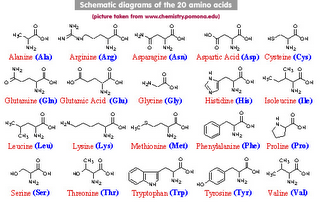
Amino Acid Properties and Substitutions
A substitution is more likely to occur between amino acids with similar biochemical properties. For example the hydrophobic amino acids Isoleucine(I) and valine(V) are more likely to substitute for one another than the hydrophilic amino acid cystine would with one of these. Amino acids come in the following types.
1. Amino acids with aliphatic hydrophobic side chains
The hydrophobic side chains of these amino acids will not form hydrogen bonds or ionic bonds with other groups. These hydrophobic amino acids tend to be buried in the centre of proteins away from the surrounding aqueous environment.
Ala, Val, Leu, lle, Met, Pro, Phe, Trp.
2. Amino acids with uncharged but polar side chains
The side chains of these amino acids are uncharged at physiological pH.
Ser, Tyr, Asp, Gln, Cys.
3. Amino acids with acidic side chains
These have a carboxylic acid group in their side chain and are very hydrophilic.
Asp, Glu.
4. Amino acids with basic side chains
The positive charge on these side chains makes them hydrophilic and they are likely to be found at the protein surface
Lys, Arg, His.
5. Neutral side chain
The single hydrogen atom side chain has no strong hydrophobic or hydrophilic properties.
Gly

Nucleotide Sequences
Nucleotide bases fall into two categories depending on the ring structure of the base. Purines (Adenine and Guanine) are two ring bases, pyrimidines (Cytosine and Thymine) are single ring bases. Mutations in DNA are changes in which one base is replaced by another. A mutation that conserves the ring number is called a transition (e.g., A -> G or C -> T) a mutation that changes the ring number are called transversions. (e.g. A -> C or A -> T and so on).
One-letter code Name Location
A Adenine DNA/RNA
G Guanine DNA/RNA
C Cytosine DNA/RNA
T Thymine DNA
U Uracil RNA
Nucleotide codes assigned by IUB
IUB Meaning Complement
A A T
C C G
G G C
T/U T A
M A/C K
R A/G Y
W A/T W
S C/G S
Y C/T R
K G/T M
V A/C/G B
H A/C/T D
D A/G/T H
B C/G/T V
X/N A/C/G/T X
. None .
Table of Standard Genetic Code
The genetic code in the table above has also been called "The Universal Genetic Code". It is known as "universal", because it is used by all known organisms as a code for DNA, mRNA, and tRNA. The universality of the genetic code encompases animals (including humans), plants, fungi, archaea, bacteria, and viruses. However, all rules have their exceptions, and such is the case with the genetic code; small variations in the code exist in mitochondria and certain microbes. Nonetheless, it should be emphasised that these variances represent only a small fraction of known cases, and that the genetic code applies quite broadly, certainly to all known nuclear genes.
Three of the codons do not specify the incorporation of any amino acids. These are known as the stop codons - UAA, UAG, UGA. They are found at the end of the mRNA coding sequence and they tell the ribosome to stop translating the message and release the protein. The mRNA is translated from the 5' end and read one codon at a time to the 3' end. Translation usually starts at a start codon (AUG) which codes for methionine.
| Second Position of Codon | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| T | C | A | G | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| F i r s t P o s i t i o n | T |
|
|
|
|
| T h i r d P o s i t i o n | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| C |
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A |
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| G |
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Full post... Related link
May 07, 2006
Google calendar: how to delete multiple entries
To get authentication:
wget -q -O- --post-data 'Email=username@gmail.com&Passwd=passwd&service=cl&source=Gulp-CalGulp-1.05' https://www.google.com/accounts/ClientLogin
Note that Auth=XXX field that comes back.
To request the feed (you can play with start-min, start-max, and max-results):
wget -q -O- --header='Authorization: GoogleLogin auth=XXX' http://www.google.com/calendar/feeds/default/private/full?start-min=2000-01-01T00:00:00&start-max=2040-01-01T23:59:59&max-results=1000
Note the edit URI's of the events you'd like to delete:
wget ... | tidy -xml -wrap 999 | grep edit
Delete the event by using its edit URI; this is a two step process, because wget does not redirect correctly:
wget -nv -O- --header='Authorization: GoogleLogin auth=XXX' --header='X-HTTP-Method-Override: DELETE' --post-data='' 'URI'
Watch the output and note the redirect URI with gsessionid attached, then execute:
wget -nv -O- --header='Authorization: GoogleLogin auth=XXX' --header='X-HTTP-Method-Override: DELETE' --post-data='' 'URI?gsessionid=YYY'
Full post... Related link
Gmail persistent links
# gmail url from atom feed:
# http://mail.google.com/mail?account_id=username%40gmail.com&message_id=10ae01bc43de52c1&view=conv&extsrc=atom
# turns into the following when you view it:
# http://mail.google.com/mail/?fs=1&tf=1&source=atom&view=cv&search=all&th=10ae01bc43de52c1
# both forms can be used as persistent urls.
To figure out the correct message_id (or th) to use, go to gmail in html view and read the link that points to your message.
This works even if you are not logged into gmail at the time, after asking for passwd etc. you are redirected to the correct message.
I should say correct conversation, these links bring up whole conversations. You can get the url pointing to an individual message in html view:
http://mail.google.com/mail/h/15ec0cgkplzcx/?d=u&n=3h&st=100&th=10ae01bc43de52c1&v=c#m_10a9636a75a772ec
But I could not make this work in a persistent format yet...
Full post...
May 06, 2006
Matrix cheat-sheet
In the discussion below:
Q,U,V: unitary matrices (QQ*=I)
S: a diagonal matrix
R: an upper triangular matrix
X: a square matrix
A = any mxn matrix
=> A = USV* (SVD decomposition)
=> A = QR (general QR-decomp with Q mxn unitary i.e. QQ*=I)
A = any nxn square matrix
=> A = QRQ* (Schur decomposition)
=> A = QR (QR decomposition)
??? What is the relation between the two?
A = diagonalizable square matrix
=> A = XSX* (Eigen or spectral decomposition)
A = normal matrix (i.e. AA* = A*A)
=> A = QSQ* (Eigenvectors orthogonal - Spectral Theorem)
subclasses of normal matrices:
A = hermitian (i.e. A*=A, means symmetric if real)
A = skew-hermitian (i.e. A*=-A, skew-symmetric if real)
A = unitary (i.e. AA*=I, orthogonal if real)
subclasses of hermitian matrices:
A = positive semidefinite (i.e. all eigenvalues nonnegative)
=> SVD and eigen decompositions are the same: singular values need to be non-negative.
A = positive definite (i.e. all eigenvalues positive)
(1) Excerpt from http://en.wikipedia.org/wiki/Spectral_decomposition
These results translate immediately into results about matrices: For any normal matrix A, there exists a unitary matrix U such that
A=U \Lambda U*
where \Lambda is the diagonal matrix the entries of which are the eigenvalues of A. Furthermore, any matrix which can be diagonalized in this way must be normal.
The column vectors of U are the eigenvectors of A and they are orthogonal.
The spectral decomposition is a special case of the Schur decomposition. It is also a special case of the singular value decomposition.
If A is a real symmetric matrix, it follows by the real version of the spectral theorem for symmetric operators that there is an orthogonal matrix U such that UAU* is diagonal and all the eigenvalues of A are real.
(2) Excerpt from http://en.wikipedia.org/wiki/Eigenvalue%2C_eigenvector_and_eigenspace#Eigenvalue_equation
Decomposition theorems for general matrices
The decomposition theorem is a version of the spectral theorem in the particular case of matrices. This theorem is usually introduced in terms of coordinate transformation. If U is an invertible matrix, it can be seen as a transformation from one coordinate system to another, with the columns of U being the components of the new basis vectors within the old basis set. In this new system the coordinates of the vector v are labeled v'. The latter are obtained from the coordinates v in the original coordinate system by the relation v' = Uv and, the other way around, we have v = U − 1v'. Applying successively v' = Uv, w' = Uw and U − 1U = I, to the relation Av = w defining the matrix multiplication provides A'v' = w' with A' = UAU − 1, the representation of A in the new basis. In this situation, the matrices A and A' are said to be similar.
The decomposition theorem states that, if one chooses as columns of U − 1 n linearly independent eigenvectors of A, the new matrix A' = UAU − 1 is diagonal and its diagonal elements are the eigenvalues of A. If this is possible the matrix A is diagonalizable. An example of non-diagonalizable matrix is given by the matrix A above. There are several generalizations of this decomposition which can cope with the non-diagonalizable case, suited for different purposes:
* the Schur triangular form states that any matrix is unitarily equivalent to an upper triangular one;
* the singular value decomposition, A = UΣV * where Σ is diagonal with U and V unitary matrices. The diagonal entries of A = UΣV * are nonnegative; they are called the singular values of A. This can be done for non-square matrices as well;
* the Jordan normal form, where A = XΛX − 1 where Λ is not diagonal but block-diagonal. The number and the sizes of the Jordan blocks are dictated by the geometric and algebraic multiplicities of the eigenvalues. The Jordan decomposition is a fundamental result. One might glean from it immediately that a square matrix is described completely by its eigenvalues, including multiplicity, up to similarity. This shows mathematically the important role played by eigenvalues in the study of matrices;
* as an immediate consequence of Jordan decomposition, any matrix A can be written uniquely as A = S + N where S is diagonalizable, N is nilpotent (i.e., such that Nq=0 for some q), and S commutes with N (SN=NS).
Full post... Related link